Access answers to Maharashtra Board Solutions For Class 8 Maths Part 1 Chapter 3- Indices and Cube Root.

Practice set 3.1 PAGE NO: 15

1. Express the following numbers in index form.
(1) Fifth root of 13
(2) Sixth root of 9
(3) Square root of 256
(4) Cube root of 17
(5) Eighth root of 100
(6) Seventh root of 30

Solution:

In general, n^th root of ‘a’ is expressed as a^1/n . where, a is the base and 1/5 is the index.

So now,

(1) Fifth root of 13

Index form of fifth root of 13is expressed as 13^1/5 .

(2) Sixth root of 9

Index form of sixth root of 9 is expressed as 9^1/6 .

(3) Square root of 256

Index form of square root of 256 is expressed as 256^1/2 .

(4) Cube root of 17

Index form of cube root of 17 is expressed as 17^1/3 .

(5) Eighth root of 100

Index form of eighth root of 100 is expressed as 100^1/8 .

(6) Seventh root of 30

Index form of seventh root of 30 is expressed as 30^1/7 .

2. Write in the form ‘n^th root of a’ in each of the following numbers.

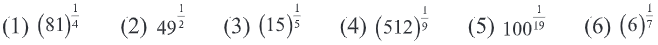
Solution:

In general, a^1/n is written as ‘n^th root of a’.

So now,

(1) (81)^1/4

(81)^1/4 is written as ‘4^th root of 81’.

(2) (49)^1/2

(49)^1/2 is written as ‘square root of 49’.

(3) (15)^1/5

(15)^1/5 is written as ‘5^th root of 15’.

(4) (512)^1/9

(512)^1/9 is written as ‘9^th root of 512’.

(5) (100)^1/19

(100)^1/19 is written as ‘19^th root of 100’.

(6) (6)^1/7

(6)^1/7 is written as ‘7^th root of 6’.

Practice set 3.2 PAGE NO: 16

1. Complete the following table.

Sr. No.	Number	Power of the root	Root of the power
(1)	(225)3/2	Cube of square root of 225	Square root of cube of 225
(2)	(45)4/5
(3)	(81)6/7
(4)	(100)4/10
(5)	(21)3/7

Solution:

Generally we can express the number a^m/n as

a^m/n = (a^m )^1/n means ‘n^th root of m^th power of a’.

a^m/n = (a^1/n )^m means ‘m^th power of n^th root of a’.

So by using the above rules let us fill the table:

Sr. No.	Number	Power of the root	Root of the power
(1)	(225)3/2	Cube of square root of 225	Square root of cube of 225
(2)	(45)4/5	Fourth power of fifth root of 45	Fifth root of fourth power of 45
(3)	(81)6/7	Sixth power of seventh root of 81	Seventh root of sixth power of 81
(4)	(100)4/10	Fourth power of tenth root of 100	Tenth root of fourth power of 100
(5)	(21)3/7	Cube of seventh root of 21	Seventh root of cube of 21

2. Write the following number in the form of rational indices.
(1) Square root of 5^th power of 121.
(2) Cube of 4^th root of 324.
(3) 5^th root of square of 264.
(4) Cube of cube root of 3.

Solution:

We know that ‘n^th root of m^th power of a’ is expressed as (a^m )^1/n .

And ‘m^th power of n^th root of a’ is expressed as (a^1/n )^m .

So by using the above rules let us find

(1) Square root of 5^th power of 121.

Square root of 5^th power of 121 is expressed as (121⁵ )^1/2 or (121)^5/2 .

(2) Cube of 4^th root of 324.

Cube of 4^th root of 324 is expressed as (324^1/4 )³ or (324)^3/4 .

(3) 5^th root of square of 264.

5^th root of square of 264 is expressed as (264² )^1/5 or (264)^2/5 .

(4) Cube of cube root of 3.

Cube of cube root of 3 is expressed as (3^1/3 )³ or (31)^3/3 .

Practice set 3.3 PAGE NO: 18

1. Find the cube root of the following numbers.

(1) 8000

(2) 729

(3) 343

(4) -512

(5) -2744

(6) 32768

Solution:

(1) 8000

Firstly let us find the factor of 8000

8000 = 2 × 2 × 2 × 2 × 2 × 2 × 5 × 5 × 5

So to find the cube root, we pair the prime factors in 3’s.

8000 = (2 × 2 × 5)³

= (2 × 10)³

= 20³

Hence, cube root of 8000 = ∛(8000)

= (20³ )^1/3

= 20

(2) 729

Firstly let us find the factor of 729

729 = 9 × 9 × 9

So to find the cube root, we pair the prime factors in 3’s.

729 = 9³

Hence, cube root of 729 = ∛(729)

= (9³ )^1/3

= 9

(3) 343

Firstly let us find the factor of 343

343 = 7 × 7 × 7

So to find the cube root, we pair the prime factors in 3’s.

343 = 7³

Hence, cube root of 343 = ∛(343)

= (7³ )^1/3

= 7

(4) -512

Firstly let us find the factor of -512

-512 = (-8) × (-8) × (-8)

So to find the cube root, we pair the prime factors in 3’s.

-512 = (-8)³

Hence, cube root of -512 = ∛(-512)

= (-8³ )^1/3

= -8

(5) -2744

Firstly let us find the factor of -2744

-2744 = (-14) × (-14) × (-14)

So to find the cube root, we pair the prime factors in 3’s.

-2744 = (-14)³

Hence, cube root of -2744 = ∛(-2744)

= (-14³ )^1/3

= -14

(6) 32768

Firstly let us find the factor of 32768

32768 = 32 × 32 × 32

So to find the cube root, we pair the prime factors in 3’s.

32768 = 32³

Hence, cube root of 32768 = ∛(32768)

= (32³ )^1/3

= 32

2. Simplify:

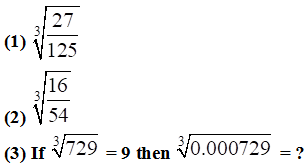
Solution:

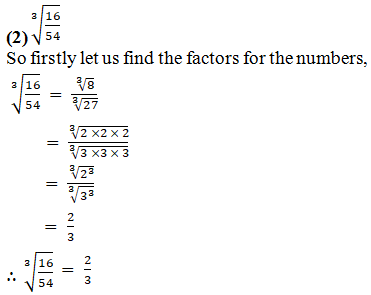
Cube roots are used in day to day Mathematics, such as in powers and exponents or to find the side of a three-dimensional cube when its volume is given. Here, many such exercise problems are given, students can practice the solutions to secure good marks in the exams.